Подготовка к ОГЭ (ГИА)

Условие задачи:
Биссектриса прямого угла прямоугольного треугольника образует с его гипотенузой угол 46°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.

Решение:

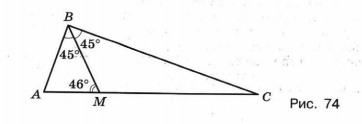
Пусть АВС — данный прямоугольный треугольник с гипотенузой АС, АСВ — его меньший угол, а биссектриса угла АВС пересекает гипотенузу в точке М (рис. 74). Тогда угол ВМА = 46°. Поскольку этот угол — внешний угол треугольника ВМС, он равен сумме углов МВС и МСВ. Таким образом, MСВ = АМВ - MВС = 46° - 45° = 1°.

Ответ: 1