Подготовка к ОГЭ (ГИА)

Условие задачи:
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC = 19, а расстояние от точки K до стороны AB равно 7.

Решение:

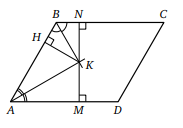
Пусть KH, KN и KM — перпендикуляры, опущенные из точки K к сторонам AB, BC и AD соответственно (см. рисунок). Тогда KM = KH = KN = 7.

Кроме того, точки M, K и N лежат на одной прямой, и высота MN параллелограмма ABCD равна MK + KN = 14.

По формуле площади параллелограмма находим

S_ABCD = BC * MN = 19 * 14 = 266.

Ответ: 266