Подготовка к ОГЭ (ГИА)

Условие задачи:

Биссектрисы углов А и В параллелограмма ABCD пересекаются в точке F стороны CD. Докажите, что F – середина CD.

Решение задачи:

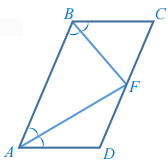
Доказательство строим на факте, что биссектриса AF делит угол BAD на два равных угла:

BAF = FAD

По правилу накрест лежащих углов при параллельных прямых AB и CD:

∠BAF = ∠ DFA.

Тогда углы FAD и DFA тоже равны, так как BAF = FAD. Значит, треугольник AFD – равнобедренный с основанием AF. Следовательно, AD = DF. По тем же причинам в треугольнике BCF BC = CF. В параллелограмме противоположные стороны равны – значит, BC = AD. Но тогда CF тоже равен AD, а значит, равен также FD. Если CF = FD, то F – середина CD.

Что и требовалось доказать.