Условие задачи:
Окружности с центрами в точках P и Q не имеют общих точек. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении a : b. Докажите, что диаметры этих окружностей относятся как a : b.
Решение задачи:
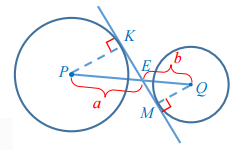
Проведем радиусы PK и QM к касательным. По определению, радиус и касательная к окружности образуют прямой угол. Значит, треугольники PKE и MEQ – прямоугольные. У них углы ЕКР и QME – прямые. Углы РЕК и QEM равны как вертикальные. Значит, третьи углы треугольников соответственно равны. Вывод: треугольники PKE и MEQ – подобны. Отметим подобные стороны:
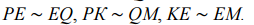
Известны величины двух подобных сторон: РЕ = а, EQ = b. Найдем коэффициент подобия двух треугольников – и одновременно определим соотношение радиусов PK и QM:
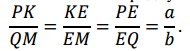
Утверждение доказано.