Подготовка к ОГЭ (ГИА)

Условие задачи:
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.

Решение:

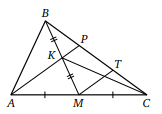
Проведём MT || AP. Тогда MT — средняя линия треугольника APC и CT = TP, а KP — средняя линия треугольника BMT и TP = BP. Обозначим площадь треугольника BKP через S. Тогда площадь треугольника KPC, имеющего ту же высоту и вдвое большее основание, равна 2S. Значит, площадь треугольника CBK равна 3S и равна площади треугольника CMK, которая в свою очередь равна площади треугольника AMK. Площадь треугольника ABK равна площади треугольника AMK. Итак.

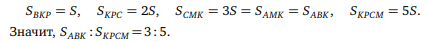
Ответ: 3:5