Два автомобиля одновременно отправляются в 930...
Условие задачи:
Из А в В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 30 км/ч, а вторую половину – со скоростью на 9 км/ч больше скорости первого, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля.
Решение задачи:
Примем за х скорость второго автомобиля. Тогда скорость первого равна х + 31. Примем за у время первого автомобиля. Тогда время второго равно у + 5. Получаем систему уравнений:
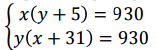
В первом уравнении, которое проще, выразим х через у:
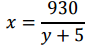
Подставим во второе уравнение:
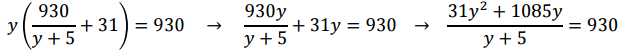
Приравняем уравнение к нулю и подведем его под общий знаменатель:
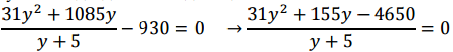
Приравняем числитель к нулю, получим квадратное уравнение и найдем его корни: y1 = −15, y2 = 10. Мы выяснили, что первый автомобиль проехал маршрут за 10 часов. Найдем его скорость:
v = 930 : 10 = 93 км/ч.
Ответ: 93