Подготовка к ОГЭ (ГИА)

Условие задачи:

Из А в В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 30 км/ч, а вторую половину – со скоростью на 9 км/ч больше скорости первого, в результате чего прибыл в В одновременно с первым автомобилем. Найдите скорость первого автомобиля. 

Решение задачи:

Примем расстояние между А и В за 1. Пусть скорость первого автомобиля равна х. Тогда скорость второго на второй половине пути равна х + 9. Время, за которое первый автомобиль проехал весь путь, составляет 1/x . Для второго автомобиля разделим путь на две равные части. То есть половина пути составляет 0,5. Время второго автомобиля на первой половине пути равно 0,5/30 = 1/60 , на второй половине пути равно 0,5/(x+9) = 1/(2(x+9)) . 

В совокупности время второго автомобиля равно сумме двух этих временных отрезков: 

Две машины приехали в В одновременно, то есть время первого автомобиля равно времени второго: 

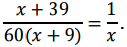
Решим уравнение: 

х(х + 39) = 60(х + 9), 

x² + 39x = 60x + 540. 

Приравняем уравнение к нулю и получим квадратное уравнение: 

x² + 39x − 60x − 540 = 0, 

x² − 21x − 540 = 0. 

Найдем корни: 

x₁ = −15; x₂ = 36. 

Скорость неотрицательна – значит, из двух полученных ответов верным является второй. 

Ответ: 36