Подготовка к ОГЭ (ГИА)

Условие задачи:
Медиана ВМ треугольника АВС является диаметром окружности, пересекающей сторону ВС в её середине. Длина стороны АС равна 4 см. Найдите радиус окружности, описанной около треугольника АВС.

Решение:

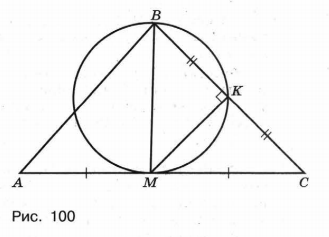
Пусть К — середина ВС. Тогда угол BKM прямой (как вписанный угол, опирающийся на диаметр). Значит, МК является медианой и высотой треугольника ВМС (рис. 100). Поэтому треугольник ВМС равнобедренный. Следовательно, МВ = МА = МС и точка М — центр окружности, описанной около треугольника АВС, радиус которой равен МС = 0,5АС = 2 см.

Ответ: 2