Условие задачи:
На рисунке 66 изображены параллельные прямые FE, MN и секущая АВ, пересекающая FE в точке С, a MN в точке D. Выполните следующие задания:
а) Установите соответствие между парами углов и их названиями.
В таблице под каждой буквой укажите номер соответствующего названия.
Пара углов
A) ACF и DCE
Б) FCD и CDM
B) ACF и АСЕ
Г) DCF и NDC
Д) ACF и CDM
Название
1) Смежные
2) Вертикальные
3) Односторонние
4) Соответственные
5) Накрест лежащие
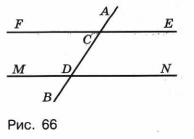
б) Найдите величину угла CDM, если известно, что она вдвое больше величины угла NDC.
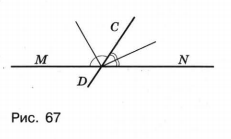
в) Найдите величину угла между биссектрисами углов CDM и NDC.
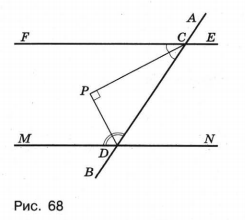
г) Найдите величину угла между биссектрисами углов FCD и CDM.
Решение:
а) Углы ACF и DCE являются вертикальными, углы FCD и CDM — односторонними, углы ACF и АСЕ — смежными, углы DCF и NDC — накрест лежащими, углы ACF и СDM — соответственными. Поэтому таблицу нужно заполнить так:
б) Углы СDM и NDC являются смежными, поэтому их сумма равна 180°. Из условия следует, что 3∠NDC = 180°, откуда ∠NDC = 60°, и, значит, ∠CDM = 120°.
в) Угол между биссектрисами углов СDM и NDC равен сумме половин этих углов. Поскольку сумма двух смежных углов равна 180°, то сумма половин этих углов будет равна 90° (рис. 67).
г) Сумма односторонних углов FCD и CDM равна 180°, а сумма половин этих углов будет равна 90°. То есть если биссектрисы этих углов пересекаются в точке Р, то сумма углов PDC и PCD будет равна 90°, поэтому и искомый угол CPD будет равен 90° (рис. 68).
Ответ: а) 23 154; б) 120; в) 90; г) 90
