Условие задачи:
На стороне ВС остроугольного треугольника АВС (АВ ≠ АС) как на диаметре построена полуокружность, пересекающая высоту AD в точке М. AD = 90, MD = 69, Н – точка пересечения высот треугольника АВС. Найдите АН.
Решение задачи:
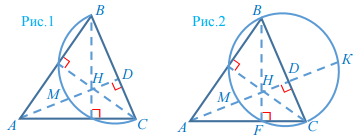
Нарисуем треугольник и полуокружность, как сказано в задаче (рис.1). Отметим точку пересечения окружности со стороной АС буквой F (рис.2) Угол BFC опирается на диаметр ВС – значит, он прямой. И значит, это одновременно высота треугольника АВС. Построим полный круг и продлим высоту AD до точки К на окружности (рис.2). ВС – диаметр, а хорда МК пересекает его под прямым углом. То есть ВС является серединным перпендикуляром, который делит любые перпендикулярные хорды пополам. Значит:
DK = MD = 69.
Отсюда:
МК = MD + DK = 69 + 69 = 138.
Если AD = 90, то:
AK = AD + DK = 90 + 69 = 159.
Если AD = 90, MD = 69, то:
AM = AD – MD = 90 – 69 = 21.
Вспомним теорему секущих:
AF ∙ AC = AM ∙ AK = 21 ∙ 159 = 3339.
Этот результат понадобится нам позже. А пока изучим треугольники AHF и ADC. У них общий угол DAC, и они оба прямоугольные треугольники – то есть, две пары углов у них равны. Значит, и третьи углы тоже равны, и это подобные треугольники. Определим подобные стороны: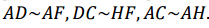
Составим пропорцию подобия только для двух сторон:
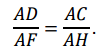
Отсюда:
AD ∙ AH = AF ∙ AC.
Нам уже известно произведение AF ∙ AC. Следовательно:
AD ∙ AH = 3339.
Так как AD = 90, то:
90 ∙ АН = 3339,
АН = 3339 : 90,
АН = 37,1.
Ответ: 37,1
