Подготовка к ОГЭ (ГИА)

Условие задачи:
Найдите площадь параллелограмма ABCD, в котором АВ = 17, AD = 15, BD = 8.

Решение:

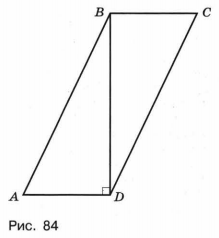
Задачу можно решать разными способами. По следствию теоремы косинусов для треугольника ABD можно найти косинус угла В, затем его синус, после чего вычислить площадь параллелограмма как произведение двух сторон на синус угла между ними. Можно заметить, что 17² = 15² + 8² = 289, и, значит, АВ² = АD² + BD². Тогда по теореме, обратной теореме Пифагора, треугольник ABD — прямоугольный с прямым углом D, т. е. диагональ BD параллелограмма является его высотой (рис. 84). Поэтому площадь параллелограмма равна S = AD * BD = 15 * 8 = 120.

Ответ: 120