Задание:
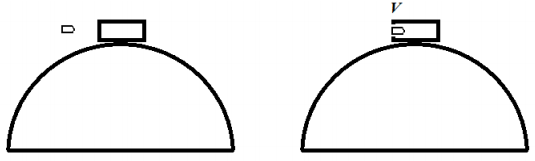
Небольшое тело массой M = 0,99 кг лежит на вершине гладкой полусферы. В тело попадает пуля массой m = 0,01 кг, летящая горизонтально со скоростью v0 = 100 м/с, и застревает в нём. Пренебрегая смещением тела за время удара, определите радиус сферы, если высота, на которой тело оторвётся от поверхности полусферы, h = 0,7 м. Высота отсчитывается от основания полусферы.
Решение:
1) Запишем закон сохранения импульса в проекции на горизонтальную ось для столкновения пули и тела
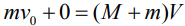
где V – скорость тела с пулей непосредственно после попадания (когда тело ещё на вершине)
Таким образом, тело с пулей начинают соскальзывать с начальной скоростью:
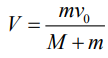
2) Запишем закон сохранения энергии, чтобы найти скорость тела на высоте h от Земли
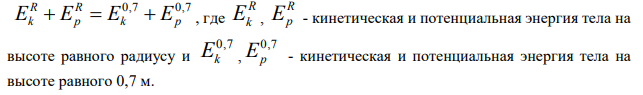
Тогда:
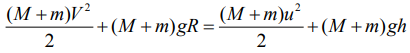
где u2 – скорость тела на высоте 0,7 м (в момент отрыва).
Заметим, что в уравнении две неизвестные – u и R. Значит необходимо ещё одно уравнение.
3) При движении тела по полусфере на него действуют сила тяжести и сила реакции опоры N
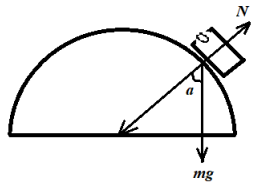
В проекции на нормаль к поверхности полусферы второй закон Ньютона имеет вид:
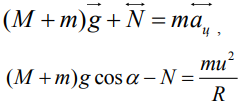
Тело оторвется от поверхности в момент, когда сила реакции опоры будет равна нулю, при этом:
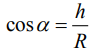
Выражаем отсюда квадрат скорости тела:
u2 = gh
4) Подставим это значение в полученное ранее уравнение и найдем радиус полусферы:
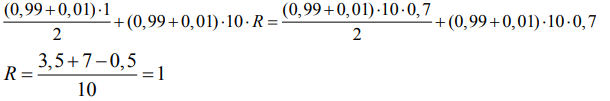
Ответ: 1 м.
