Окружность пересекает стороны AB и AC треугольника ABC...
Матемаматика ОГЭ: решения задач | Просмотров: 673 | Дата: 17.03.2018 |
Условие задачи:
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 6, а сторона AC в 1,5 раза больше стороны BC.
Решение:
Четырёхугольник BKPC вписан в окружность, значит, ∠KBC + ∠KPC = 180°. Углы APK и CPK смежные, значит, их сумма также равна 180°. Получаем, что ∠KBC = ∠APK.
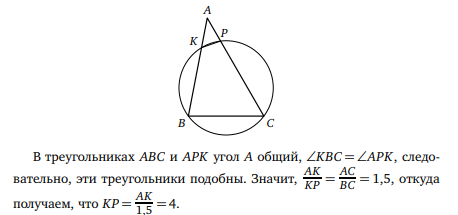
Ответ: 4
Комментарии
Всего комментариев: 0
