Подготовка к ОГЭ (ГИА)

Условие задачи:
Расстояние от центра окружности до хорды длиной 16 равно 6. Найдите радиус окружности.

Решение:

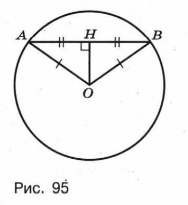
Пусть АВ — данная хорда окружности с центром О (рис. 95). Тогда ОА = ОВ (как радиусы). Поскольку треугольник ОАВ равнобедренный, его высота ОН (которая является также медианой и биссектрисой) и будет расстоянием от центра окружности до хорды. Значит, ОН = 6, АН = 8, а искомый радиус ОА находится по теореме Пифагора для треугольника ОНА: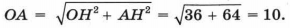 

Ответ: 10