Решите уравнение (x^2 - 16)^2 + (x^2 + x - 12)^2 = 0
Матемаматика ОГЭ: решения задач | Дата: 20.02.2017 |
Условие задачи:
Решите уравнение (x2 - 16)2 + (x2 + x - 12)2 = 0
Решение:
Любое число в квадрате всегда больше 0, следовательно, уравнение будет равно 0, если оба слагаемых равны 0. Это условие можно записать в виде следующей системы:
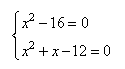
Из первого уравнения получаем два корня:
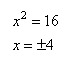
Из второго уравнения, имеем корни:
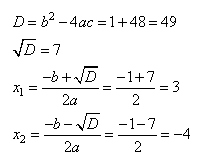
Общий корень, при котором оба уравнения переходят в 0, равен -4.
Ответ: -4
Комментарии
Всего комментариев: 0