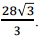Середина М стороны AD выпуклого четырехугольника ABCD...
Условие задачи:
Середина М стороны AD выпуклого четырехугольника ABCD равноудалена от всех его вершин. Найдите AD, если ВС = 14, а углы В и С четырехугольника равны соответственно 110° и 100°.
Решение задачи:
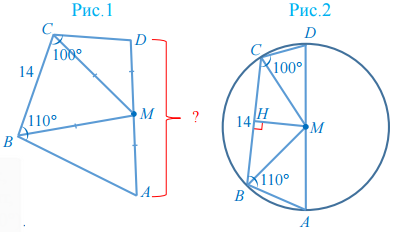
Неизвестно, каков заданный четырехугольник, поэтому пока нарисуем произвольный (рис.1). По условию задачи MD = MC = MB = MA. Несложно сделать вывод, что М – центр описанной окружности, а перечисленные отрезки являются ее радиусами. А наш четырехугольник выглядит примерно так, как показано на рисунке 2. В окружность можно вписать только такой четырехугольник, у которого сумма противоположных углов равна 180°. Значит, угол А, противоположный углу С, равен 80° (180° – 100° = 80°). Треугольник МВА – равнобедренный с основанием АВ. Значит, угол МВА тоже равен 80°. Треугольник МВС – тоже равнобедренный с основанием ВС, углы при основании равны:
∠СВМ = ∠МСВ = 110° – 80° = 30°.
Из вершины М проведем высоту МН. В равнобедренном треугольнике высота, проведенная из вершины, делит основание пополам. Значит, в прямоугольном треугольник ВНМ известен один из катетов: ВН = 7. С помощью формулы для косинусов найдем гипотенузу ВМ:
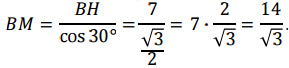
ВМ – это радиус описанной окружности, а AD – ее диаметр. Значит:
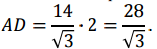
Мы получили ответ. Но в ответах тестовых заданий И.В.Ященко приведена иная запись ответа. Дело в том, что в математике принято преобразовывать дробь так, чтобы в знаменателе было число без знака корня. Умножим числитель и знаменатель полученной дроби на 3 и получим тождественную дробь:
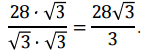
Но заметим: первая запись ответа – тоже верная!
Ответ:
