Сторона AD параллелограмма ABCD вдвое больше стороны AB...
Задание:
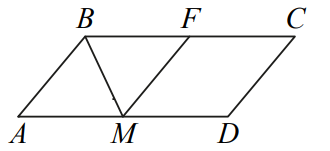
Сторона AD параллелограмма ABCD вдвое больше стороны AB. Точка M — середина стороны AD. Докажите, что BM — биссектриса угла ABC.
Доказательство:
Проведём прямую MF параллельно стороне AB (см. рисунок). Поскольку AM = MD = AB, параллелограмм ABFM является ромбом, поэтому диагональ BM ромба ABFM делит угол ABF пополам. Значит, BM — биссектриса угла ABC.
| Критерии оценивания выполнения задания |
Баллы |
| Доказательство верное, все шаги обоснованы |
2 |
| Доказательство в целом верное, но содержит неточности |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше |
0 |
| Максимальный балл |
2 |
Комментарии
Всего комментариев:
0