Подготовка к ОГЭ (ГИА)

Условие задачи:

Углы В и С треугольника АВС равны соответственно 71° и 79°. Найдите ВС, если радиус окружности, описанной около треугольника АВС, равен 8. 

Решение задачи:

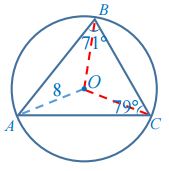
Найдем третий угол треугольника:

∠А = 180° – ∠В – ∠С = 180° – 71° – 79° = 30°.

Угол А является вписанным, он опирается на ту же дугу, что и центральный угол ВОС. Центральный угол вдвое больше соответственного вписанного – значит, ∠ВОС = 60°. Радиусы ОВ и ОС образуют равнобедренный треугольник СОВ. Углы при основании равны. Найдем их:

∠ОВС = ∠ОСВ = (180 – 60) : 2 = 60°.

Оказывается, все углы треугольника СОВ равны 60° – то есть это равносторонний треугольник. А у равностороннего треугольника все стороны равны:

ВС = ОВ = ОС = 8.

Ответ: 8