В равнобедренную трапецию, периметр которой равен 40...
Условие задачи:
В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до ее меньшего основания.
Решение задачи:
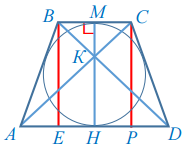
Нарисуем трапецию. Надо найти КМ. Окружность можно вписать только в такой четырехугольник, у которого суммы длин противоположных сторона равны. Значит: АВ + CD = BC + AD. Пусть BC + AD = х, АВ + CD = у. Тогда x = y = 40 : 2 = 20. Через формулу площади найдем высоту трапеции:
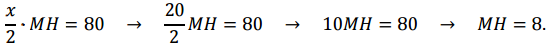
Так как трапеция равнобедренная, то АВ = CD. Значит, можем узнать и длины боковых сторон:
AB = CD = 20 : 2 = 10.
Проведем высоту трапеции от угла В. Получим прямоугольный треугольник АВЕ. В нем известны катет ВЕ и гипотенуза АВ. По теореме Пифагора найдем второй катет:
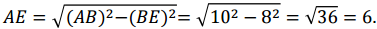
По определению равнобедренной трапеции, отрезок ED равен средней линии:
ED = 20 : 2 = 10.
Значит, большее основание AD равно АЕ + ED = 6 + 10 = 16. Найдем меньшее основание. Так АЕ = PD = 6, то ВС = ЕР = AD – AE – PD = 16 – 6 – 6 = 4.
В трапеции треугольники при основаниях, образованные диагоналями, подобны: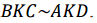 
. В двух этих треугольниках стороны AD и BC подобны. Найдем коэффициент подобия:
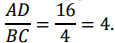
Это значит, что КМ в 4 раза меньше КН. Пусть КМ = а. Тогда КН = 4а. Получаем простое уравнение и решаем его:
а + 4а = 8,
5а = 8,
а = 1,6.
Ответ: 1,6
